Superposition d’états dans un puits de potentiel infini
Contexte : Le cœur de l'étrangeté quantique.
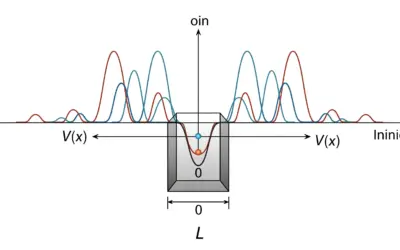
Le puits de potentiel infiniModèle fondamental en mécanique quantique décrivant une particule confinée dans une région de l'espace d'où elle ne peut s'échapper. C'est "une boîte pour particules quantiques". est l'un des problèmes les plus simples mais les plus instructifs de la mécanique quantique. Il montre que le confinement d'une particule mène à la quantification de son énergie. Cependant, la véritable puissance de la théorie quantique réside dans le principe de superpositionPostulat fondamental stipulant qu'une particule peut exister dans une combinaison de plusieurs états propres (par exemple, plusieurs niveaux d'énergie) simultanément, tant qu'aucune mesure n'est effectuée.. Une particule n'est pas obligée d'être dans un seul niveau d'énergie ; elle peut être dans une combinaison de plusieurs niveaux à la fois. Cet exercice explore les conséquences dynamiques d'un tel état de superposition, montrant que, contrairement aux états stationnaires, la probabilité de trouver la particule évolue de manière non triviale au cours du temps.
Remarque Pédagogique : Cet exercice va au-delà du simple calcul des niveaux d'énergie. Il aborde la dynamique quantique. Nous allons construire un état qui n'est pas un état propre de l'énergie et observer comment il évolue. C'est la clé pour comprendre des phénomènes comme les battements quantiques, les oscillations de saveur des neutrinos, et le fonctionnement des ordinateurs quantiques, où les qubits sont précisément des systèmes à deux niveaux en superposition.
Objectifs Pédagogiques
- Appliquer la condition de normalisationProcédure mathématique qui assure que la probabilité totale de trouver la particule quelque part dans l'univers est égale à 1 (ou 100%). C'est une exigence fondamentale pour toute fonction d'onde. à une fonction d'onde en superposition.
- Calculer la valeur moyenne (ou espérance)La valeur moyenne d'une grandeur physique (comme l'énergie) que l'on obtiendrait si on effectuait un très grand nombre de mesures sur des systèmes identiques préparés dans le même état quantique. de l'énergie pour un état non-stationnaire.
- Construire la fonction d'onde dépendant du temps \(\Psi(x, t)\) à partir de l'état initial.
- Calculer la densité de probabilité et observer son évolution temporelle.
- Comprendre la différence fondamentale entre un état stationnaire et un état de superposition.
Données de l'étude
Schéma du Puits de Potentiel Infini
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Masse de l'électron | \(m\) | \(9.109 \times 10^{-31}\) | \(\text{kg}\) |
| Largeur du puits | \(L\) | \(1.0 \times 10^{-10}\) | \(\text{m}\) (1 Å) |
| Constante de Planck | \(h\) | \(6.626 \times 10^{-34}\) | \(\text{J}\cdot\text{s}\) |
| Constante de Planck réduite | \(\hbar\) | \(1.054 \times 10^{-34}\) | \(\text{J}\cdot\text{s}\) |
Questions à traiter
- Déterminer la constante de normalisation \(A\) pour que \(\Psi(x, 0)\) soit une fonction d'onde valide.
- Calculer la valeur moyenne de l'énergie \(\langle E \rangle\) de l'électron dans cet état à \(t=0\).
- Écrire l'expression complète de la fonction d'onde \(\Psi(x, t)\) pour tout instant \(t > 0\).
- Calculer la densité de probabilité \(|\Psi(x, t)|^2\) et identifier le terme qui la fait osciller dans le temps.
Les bases de la superposition quantique
Avant la correction, revoyons les concepts clés de l'évolution des états quantiques.
1. Normalisation et Interprétation Probabiliste :
Selon l'interprétation de Born, le carré du module de la fonction d'onde, \(|\Psi(x, t)|^2\), représente la densité de probabilité de trouver la particule à la position \(x\) à l'instant \(t\). Puisque la particule doit se trouver quelque part, l'intégrale de cette densité sur tout l'espace doit être égale à 1. Cette condition, \(\int |\Psi|^2 dx = 1\), est appelée condition de normalisation.
2. Évolution Temporelle des États Propres :
Si une particule est dans un état propre de l'énergie \(\psi_n(x)\) avec l'énergie \(E_n\), son évolution temporelle est très simple. La fonction d'onde complète est \(\Psi_n(x, t) = \psi_n(x) e^{-iE_n t / \hbar}\). La densité de probabilité \(|\Psi_n(x, t)|^2 = |\psi_n(x)|^2\) est alors indépendante du temps. C'est pour cela que ces états sont appelés "stationnaires".
3. Évolution d'un État de Superposition :
Si l'état initial est une superposition, \(\Psi(x, 0) = \sum_n c_n \psi_n(x)\), alors l'évolution temporelle est obtenue en appliquant le facteur de phase à chaque composante : \(\Psi(x, t) = \sum_n c_n \psi_n(x) e^{-iE_n t / \hbar}\). Lorsque l'on calcule la densité de probabilité \(|\Psi(x, t)|^2\), des termes croisés apparaissent, contenant des facteurs comme \(e^{-i(E_n - E_m)t / \hbar}\). Ces termes d'interférence font osciller la probabilité dans le temps.
Correction : Superposition d’états dans un puits de potentiel infini
Question 1 : Déterminer la constante de normalisation (A)
Principe (le concept physique)
La normalisation est l'incarnation mathématique de l'idée que la probabilité totale de trouver la particule n'importe où dans l'univers doit être de 100%. On ajuste l'amplitude globale de la fonction d'onde (via la constante A) pour que l'intégrale de la densité de probabilité sur tout l'espace soit exactement égale à 1. C'est une étape fondamentale pour que la fonction d'onde ait un sens physique.
Mini-Cours (approfondissement théorique)
Les fonctions propres \(\psi_n(x)\) d'un système quantique forment une base "orthonormée". Cela signifie que non seulement elles sont normalisées (\(\int |\psi_n|^2 dx = 1\)), mais elles sont aussi orthogonales entre elles (\(\int \psi_m^* \psi_n dx = 0\) si \(m \neq n\)). Cette propriété simplifie énormément le calcul de normalisation pour un état de superposition.
Remarque Pédagogique (le conseil du professeur)
La normalisation, c'est un peu comme s'assurer que toutes les parts d'un gâteau totalisent bien 100% du gâteau. Si vous avez un état qui est "un peu de \(\psi_1\)" et "un peu de \(\psi_2\)", la constante de normalisation ajuste ces "un peu" pour que la somme totale des probabilités soit bien de 1.
Normes (la référence réglementaire)
L'interprétation probabiliste de la fonction d'onde et la condition de normalisation qui en découle sont des piliers de l'interprétation de Copenhague de la mécanique quantique, qui est le cadre standard enseigné et utilisé par la grande majorité des physiciens.
Formule(s) (l'outil mathématique)
La condition de normalisation s'écrit :
En utilisant l'orthonormalité des \(\psi_n\), \(\int \psi_m^* \psi_n dx = \delta_{mn}\) (où \(\delta_{mn}\) est le symbole de Kronecker).
Hypothèses (le cadre du calcul)
On suppose que la constante de normalisation \(A\) est un nombre réel positif. En général, elle peut être complexe, mais sa phase globale n'a pas de conséquence physique, on la choisit donc réelle par simplicité.
Donnée(s) (les chiffres d'entrée)
- État initial : \(\Psi(x, 0) = A (\psi_1(x) + \psi_2(x))\)
- Les \(\psi_n(x)\) sont des fonctions propres orthonormées.
Astuces(Pour aller plus vite)
Grâce à l'orthonormalité, lorsque vous développez \(|\Psi|^2 = A^2(\psi_1+\psi_2)^*(\psi_1+\psi_2)\), les termes croisés comme \(\int \psi_1^* \psi_2 dx\) seront nuls. Seuls les termes "carrés" \(\int |\psi_1|^2 dx\) et \(\int |\psi_2|^2 dx\) survivront, et ils valent 1. Le calcul devient alors très rapide.
Schéma (Avant les calculs)
Superposition des deux premiers états
Calcul(s) (l'application numérique)
On applique la condition de normalisation :
Grâce à l'orthonormalité, les deux derniers termes sont nuls, et les deux premiers valent 1 :
En choisissant A réel et positif :
Schéma (Après les calculs)
Fonction d'onde normalisée
Réflexions (l'interprétation du résultat)
Le résultat \(A = 1/\sqrt{2}\) signifie que l'état est une superposition "équiprobable" des états 1 et 2. Si on mesurait l'énergie de la particule, on aurait 50% de chance de trouver \(E_1\) (et la particule "s'effondrerait" dans l'état \(\psi_1\)) et 50% de chance de trouver \(E_2\) (et la particule s'effondrerait dans l'état \(\psi_2\)).
Points de vigilance (les erreurs à éviter)
Ne pas oublier le carré du module ! C'est \(|A|^2\) qui apparaît dans l'intégrale. Si la constante \(A\) était complexe, par exemple \(A = i/\sqrt{2}\), \(|A|^2\) serait toujours \(1/2\). De plus, ne supposez pas que la constante est toujours \(1/\sqrt{2}\). Si la superposition était \(A(\psi_1 + 2\psi_2)\), le calcul serait différent.
Points à retenir (permettre a l'apprenant de maitriser la question)
- La normalisation assure que la probabilité totale est 1.
- On intègre le carré du module de la fonction d'onde sur tout l'espace.
- L'orthonormalité des états propres simplifie grandement le calcul.
Le saviez-vous ? (la culture de l'ingénieur)
En informatique quantique, un qubit est la version quantique d'un bit. Alors qu'un bit classique est soit 0, soit 1, un qubit peut être dans une superposition \(\alpha|0\rangle + \beta|1\rangle\). La condition de normalisation est alors \(|\alpha|^2 + |\beta|^2 = 1\), où \(|\alpha|^2\) est la probabilité de mesurer 0 et \(|\beta|^2\) celle de mesurer 1.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)
Quelle serait la constante de normalisation \(A\) pour l'état \(\Psi(x,0) = A(3\psi_1 + 4\psi_2)\) ?
Question 2 : Calculer la valeur moyenne de l'énergie \(\langle E \rangle\)
Principe (le concept physique)
Lorsqu'un système est dans une superposition d'états d'énergie, une mesure de son énergie ne donnera pas une valeur intermédiaire, mais l'une des énergies propres (\(E_1\) ou \(E_2\)). La valeur moyenne \(\langle E \rangle\) n'est pas une énergie que la particule peut "avoir", mais la moyenne statistique des résultats que l'on obtiendrait sur un grand nombre de mesures. Elle représente l'énergie moyenne du système avant la mesure.
Mini-Cours (approfondissement théorique)
Pour un état \(\Psi = \sum_n c_n \psi_n\), la valeur moyenne d'un observable \(O\) est donnée par \(\langle O \rangle = \int \Psi^* \hat{O} \Psi dx\). Pour l'énergie, \(\hat{O} = \hat{H}\). Comme \(\hat{H}\psi_n = E_n\psi_n\), le calcul se simplifie grâce à l'orthonormalité en \(\langle E \rangle = \sum_n |c_n|^2 E_n\). C'est une somme pondérée des énergies possibles, où les poids sont les probabilités \(|c_n|^2\) de trouver chaque énergie.
Remarque Pédagogique (le conseil du professeur)
Imaginez un dé spécial qui donne "1" la moitié du temps et "6" l'autre moitié. Un seul lancer donnera soit 1, soit 6. Mais la valeur moyenne sur de nombreux lancers sera \((0.5 \times 1) + (0.5 \times 6) = 3.5\). Notre état quantique est similaire : la mesure donne \(E_1\) ou \(E_2\), mais la valeur moyenne est \(\langle E \rangle = P(E_1)E_1 + P(E_2)E_2\).
Normes (la référence réglementaire)
Le calcul des valeurs moyennes (ou espérances) via la formule \(\langle O \rangle = \int \Psi^* \hat{O} \Psi dx\) est l'un des postulats fondamentaux de la mécanique quantique, qui relie l'appareil mathématique (fonctions d'onde, opérateurs) aux résultats expérimentaux (valeurs mesurées).
Formule(s) (l'outil mathématique)
Pour un état normalisé \(\Psi(x, 0) = \frac{1}{\sqrt{2}}(\psi_1 + \psi_2)\) :
où \(c_1 = c_2 = 1/\sqrt{2}\).
Hypothèses (le cadre du calcul)
On calcule la valeur moyenne à l'instant \(t=0\). Comme l'énergie est conservée, cette valeur moyenne restera constante au cours du temps, même si la fonction d'onde, elle, évolue.
Donnée(s) (les chiffres d'entrée)
- Probabilité de trouver \(E_1\), \(P_1 = |c_1|^2 = (1/\sqrt{2})^2 = 1/2\)
- Probabilité de trouver \(E_2\), \(P_2 = |c_2|^2 = (1/\sqrt{2})^2 = 1/2\)
- Énergies : \(E_n = n^2 h^2 / (8mL^2)\)
Astuces(Pour aller plus vite)
Calculez d'abord l'énergie de l'état fondamental, \(E_1\). Les autres énergies sont simplement des multiples : \(E_n = n^2 E_1\). Cela simplifie grandement les calculs. Ici, \(E_2 = 2^2 E_1 = 4E_1\).
Schéma (Avant les calculs)
Mesure de l'Énergie
Calcul(s) (l'application numérique)
1. Calculer l'énergie de l'état fondamental \(E_1\) :
2. Calculer l'énergie du premier état excité \(E_2 = 4E_1\) :
3. Calculer la valeur moyenne :
Schéma (Après les calculs)
Valeur Moyenne de l'Énergie
Réflexions (l'interprétation du résultat)
La valeur moyenne de l'énergie, \(2.5 E_1\), n'est ni \(E_1\) ni \(E_2\). C'est une valeur qui n'est même pas une énergie permise pour un état stationnaire ! Cela souligne que \(\langle E \rangle\) est une moyenne statistique, pas une valeur que le système possède réellement avant la mesure.
Points de vigilance (les erreurs à éviter)
N'oubliez pas d'utiliser les coefficients au carré (\(|c_n|^2\)) pour les probabilités. Ici, \((1/\sqrt{2})^2 = 1/2\). Une erreur fréquente est d'oublier de mettre au carré et d'utiliser \(1/\sqrt{2}\) comme probabilité, ce qui est incorrect.
Points à retenir (permettre a l'apprenant de maitriser la question)
- La valeur moyenne de l'énergie est la somme pondérée des énergies propres.
- Les poids sont les probabilités \(|c_n|^2\) d'obtenir chaque énergie.
- \(\langle E \rangle\) n'est pas nécessairement une des énergies permises du système.
Le saviez-vous ? (la culture de l'ingénieur)
Dans les lasers, on "pompe" les atomes pour les amener dans un état excité. Ils se désexcitent en émettant des photons. Si on prépare les atomes dans une superposition cohérente d'états, on peut obtenir une émission stimulée où tous les photons sont émis en phase, créant le faisceau laser intense et cohérent.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)
Quelle serait la valeur moyenne \(\langle E \rangle\) (en termes de \(E_1\)) pour l'état normalisé \(\Psi = \frac{3}{5}\psi_1 + \frac{4}{5}\psi_2\) ?
Question 3 : Écrire l'expression complète de la fonction d'onde \(\Psi(x, t)\)
Principe (le concept physique)
La fonction d'onde contient toute l'information sur un système quantique. Son évolution dans le temps est régie par l'équation de Schrödinger. Pour un état de superposition, chaque composante de l'état évolue indépendamment avec sa propre "horloge" quantique, dont la vitesse est déterminée par son énergie propre. La fonction d'onde à un instant \(t\) est la somme de ces composantes évoluées.
Mini-Cours (approfondissement théorique)
L'opérateur d'évolution temporelle \( \hat{U}(t) = e^{-i\hat{H}t/\hbar} \) fait évoluer un état de \(t=0\) à un instant \(t\) : \( |\Psi(t)\rangle = \hat{U}(t) |\Psi(0)\rangle \). Si \(|\Psi(0)\rangle\) est une superposition d'états propres de \(\hat{H}\), alors l'action de l'opérateur est simple : \( e^{-i\hat{H}t/\hbar} \sum_n c_n |\psi_n\rangle = \sum_n c_n (e^{-iE_nt/\hbar}) |\psi_n\rangle \). Chaque état propre accumule simplement un facteur de phase complexe qui dépend de son énergie.
Remarque Pédagogique (le conseil du professeur)
Imaginez deux coureurs sur une piste circulaire, partant du même point mais courant à des vitesses différentes. Leur position relative change constamment. C'est la même chose pour notre superposition : les composantes \(\psi_1\) et \(\psi_2\) sont les "coureurs", et leurs énergies \(E_1\) et \(E_2\) sont leurs "vitesses". Le facteur de phase \(e^{-iEt/\hbar}\) décrit leur "position" sur un cercle complexe. La fonction d'onde totale est la somme de ces deux "coureurs" en constante évolution relative.
Normes (la référence réglementaire)
L'évolution temporelle de la fonction d'onde via l'équation de Schrödinger dépendante du temps, \( i\hbar \frac{\partial}{\partial t}\Psi = \hat{H}\Psi \), est le postulat le plus fondamental de la dynamique quantique.
Formule(s) (l'outil mathématique)
Si \(\Psi(x, 0) = \sum_n c_n \psi_n(x)\), alors :
Hypothèses (le cadre du calcul)
On suppose que le potentiel du puits est indépendant du temps, ce qui garantit que les énergies propres \(E_n\) sont constantes et que cette méthode d'évolution est valide.
Donnée(s) (les chiffres d'entrée)
- \(\Psi(x, 0) = \frac{1}{\sqrt{2}}(\psi_1(x) + \psi_2(x))\)
- \(\psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right)\)
- \(E_n = n^2 E_1\)
Astuces(Pour aller plus vite)
Il n'y a pas de calcul complexe ici, il s'agit simplement d'appliquer la "recette" de l'évolution temporelle : prendre chaque terme de la superposition à \(t=0\) et le multiplier par le facteur de phase \(e^{-iE_n t / \hbar}\) correspondant.
Schéma (Avant les calculs)
Évolution des Composantes
Calcul(s) (l'application numérique)
On applique directement la formule de l'évolution temporelle à notre état :
Schéma (Après les calculs)
Phases Complexes Évolutives
Réflexions (l'interprétation du résultat)
Cette expression est la description la plus complète possible de l'état de l'électron. Elle contient à la fois l'information spatiale (via les fonctions sinus) et l'information temporelle (via les exponentielles complexes). C'est à partir de cette fonction que toutes les autres propriétés observables (probabilité, valeur moyenne de la position, etc.) peuvent être calculées à n'importe quel instant.
Points de vigilance (les erreurs à éviter)
Assurez-vous de bien faire correspondre chaque fonction propre \(\psi_n\) avec son énergie propre \(E_n\) dans l'exponentielle. Mélanger les énergies (par exemple, associer \(\psi_1\) avec \(e^{-iE_2t/\hbar}\)) est une erreur qui viole l'équation de Schrödinger.
Points à retenir (permettre a l'apprenant de maitriser la question)
- L'évolution temporelle d'une superposition se fait en appliquant le facteur de phase \(e^{-iE_n t / \hbar}\) à chaque composante \(c_n\psi_n\).
- Chaque composante évolue à un "rythme" dicté par son énergie propre.
- La fonction \(\Psi(x, t)\) est la solution de l'équation de Schrödinger dépendante du temps.
Le saviez-vous ? (la culture de l'ingénieur)
L'horloge atomique, l'instrument de mesure du temps le plus précis jamais créé, est basée sur ce principe. On place des atomes dans une superposition de deux niveaux d'énergie très proches et on mesure la fréquence d'oscillation de cette superposition, qui est incroyablement stable et définit la seconde.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)
Quelle serait la fonction d'onde \(\Psi(x,t)\) pour l'état initial normalisé \(\Psi(x,0) = \frac{1}{\sqrt{2}}(\psi_1 - \psi_3)\) ?
Question 4 : Calculer la densité de probabilité \(|\Psi(x, t)|^2\)
Principe (le concept physique)
La densité de probabilité nous dit où la particule a le plus de chances d'être trouvée si on la mesure. Pour un état stationnaire, cette carte de probabilité est fixe. Pour une superposition, les différentes composantes de la fonction d'onde "interfèrent" les unes avec les autres. Comme leurs phases relatives évoluent dans le temps, leurs interférences (parfois constructives, parfois destructives) changent aussi, ce qui fait que la carte de probabilité se met à osciller.
Mini-Cours (approfondissement théorique)
Le calcul de \(|\Psi|^2 = \Psi^* \Psi\) pour une superposition \(\Psi = c_1\Psi_1 + c_2\Psi_2\) donne \(|c_1|^2|\Psi_1|^2 + |c_2|^2|\Psi_2|^2 + c_1^*c_2\Psi_1^*\Psi_2 + c_1c_2^*\Psi_1\Psi_2^*\). Les deux premiers termes sont les densités de probabilité stationnaires. Les deux derniers sont les termes d'interférence. En utilisant \(e^{i\theta} = \cos\theta + i\sin\theta\), on peut montrer que ces termes d'interférence oscillent avec une fréquence angulaire \(\omega = (E_2-E_1)/\hbar\).
Remarque Pédagogique (le conseil du professeur)
C'est comme accorder une guitare. Quand deux cordes sont presque accordées, vous entendez un "battement" (une oscillation lente du volume sonore). Ce battement est dû à l'interférence entre les deux ondes sonores. La densité de probabilité de notre électron subit exactement le même phénomène : un "battement quantique" dû à l'interférence entre les deux ondes de matière \(\psi_1\) et \(\psi_2\).
Normes (la référence réglementaire)
L'existence de termes d'interférence dans la densité de probabilité est une conséquence directe de la linéarité de l'équation de Schrödinger et du principe de superposition. C'est l'une des prédictions les plus fondamentales et les mieux vérifiées de la théorie quantique, observée dans d'innombrables expériences.
Formule(s) (l'outil mathématique)
On calcule le carré du module de la fonction d'onde :
Hypothèses (le cadre du calcul)
Les calculs sont directs et ne nécessitent pas d'hypothèses supplémentaires par rapport à celles déjà faites.
Donnée(s) (les chiffres d'entrée)
- \(\Psi(x, t) = \frac{1}{\sqrt{2}} \left( \psi_1 e^{-iE_1 t / \hbar} + \psi_2 e^{-iE_2 t / \hbar} \right)\)
Astuces(Pour aller plus vite)
Utilisez l'identité d'Euler \(e^{i\theta} + e^{-i\theta} = 2\cos\theta\). Lorsque vous développerez \(\Psi^*\Psi\), des termes comme \(e^{i(E_2-E_1)t/\hbar} + e^{-i(E_2-E_1)t/\hbar}\) apparaîtront, ce qui se simplifiera directement en un cosinus, révélant l'oscillation.
Schéma (Avant les calculs)
Interférence des Ondes de Matière
Calcul(s) (l'application numérique)
1. Écrire \(\Psi^*\) et \(\Psi\) :
2. Développer le produit \(\Psi^*\Psi\) :
3. Utiliser l'identité d'Euler pour simplifier :
Schéma (Après les calculs)
Densité de Probabilité Oscillante
Réflexions (l'interprétation du résultat)
La densité de probabilité n'est pas statique. Elle est composée d'une partie stationnaire (\(\frac{1}{2}(\psi_1^2 + \psi_2^2)\)) et d'une partie oscillante, le terme d'interférence. Ce terme en cosinus fait "bouger" la probabilité d'un côté à l'autre du puits, avec une fréquence angulaire \(\omega = (E_2-E_1)/\hbar\). La particule n'est pas immobile, sa localisation probable oscille dans le temps.
Points de vigilance (les erreurs à éviter)
Une erreur courante est de calculer \(|\Psi|^2\) comme \(|\psi_1|^2 + |\psi_2|^2\). C'est faux ! C'est précisément l'oubli des termes d'interférence qui fait perdre toute la physique de la superposition. Rappelez-vous toujours que \(|A+B|^2 \neq |A|^2 + |B|^2\) pour les nombres complexes.
Points à retenir (permettre a l'apprenant de maitriser la question)
- La densité de probabilité d'un état de superposition n'est PAS la somme des densités de probabilité.
- Elle contient des termes d'interférence qui dépendent du temps.
- Ces termes oscillent à une fréquence proportionnelle à la différence d'énergie entre les états superposés.
Le saviez-vous ? (la culture de l'ingénieur)
Les "quantum dots" sont de minuscules cristaux semi-conducteurs (quelques nanomètres) qui agissent comme des puits de potentiel pour les électrons. En changeant la taille du cristal, on change la largeur du puits \(L\), et donc les énergies \(E_n\). Cela permet de contrôler précisément la couleur de la lumière émise, une technologie utilisée dans les écrans QLED.
FAQ (pour lever les doutes)
Résultat Final (la conclusion chiffrée)
A vous de jouer(pour verifier la comprehension de l'etudiant parrapport a la question)
À quelle fréquence angulaire \(\omega\) (en termes de \(E_1\) et \(\hbar\)) la densité de probabilité oscillerait-elle pour une superposition de \(\psi_1\) et \(\psi_3\) ?
Outil Interactif : Dynamique de la Superposition
Visualisez l'évolution de la densité de probabilité au cours du temps.
Paramètres de la Simulation
Propriétés du Puits
Le Saviez-Vous ?
L'expérience de la double fente est l'illustration la plus célèbre de la superposition et de l'interférence. Un électron unique, envoyé vers deux fentes, passe "par les deux à la fois" (il est dans une superposition des états "passe par la fente de gauche" et "passe par la fente de droite"). Ces deux chemins interfèrent pour créer une figure d'interférence sur l'écran, même si les électrons sont envoyés un par un.
Foire Aux Questions (FAQ)
Que signifie "mesurer l'énergie" ?
En pratique, cela signifie faire interagir le système (l'électron dans le puits) avec un appareil de mesure. Par exemple, on pourrait essayer de lui faire émettre un photon. L'énergie du photon émis nous renseignerait sur la différence d'énergie entre l'état initial et final de l'électron. L'acte de mesure force le système à "choisir" l'un de ses états propres d'énergie. C'est ce qu'on appelle la "réduction du paquet d'onde".
Pourquoi la phase complexe est-elle si importante ?
Dans un état stationnaire, la phase globale \(e^{-iEt/\hbar}\) n'a pas d'importance car elle disparaît dans le calcul de \(|\Psi|^2\). Mais dans une superposition, c'est la *différence* de phase entre les composantes qui compte. C'est cette différence de phase, qui évolue dans le temps, qui crée les phénomènes d'interférence et la dynamique non-triviale du système.
Quiz Final : Testez vos connaissances
1. Un électron est dans un état stationnaire \(\psi_3\). Sa densité de probabilité...
2. On prépare un état de superposition entre \(\psi_1\) et \(\psi_4\). La densité de probabilité oscillera à une fréquence proportionnelle à :
- État Stationnaire
- Un état quantique dont la densité de probabilité est constante dans le temps. Ce sont les états propres de l'opérateur Hamiltonien (énergie).
- Superposition
- Un état quantique qui est une combinaison linéaire de plusieurs états stationnaires. Sa densité de probabilité évolue généralement dans le temps.
- Valeur Moyenne (Espérance)
- La moyenne statistique des résultats d'une mesure d'une grandeur physique, obtenue sur un grand nombre de systèmes identiques.
D’autres exercices de physique quantique:
0 commentaires